假设检验的两类错误-功效分析和样本量预估

发表于 | 分类于 ， | | 阅读次数:

一个对比实验，需要多大的样本量才能确保统计结果可信？做完实验后，如何判断其结果的显著性？而结果显著性的这个结论，又有多大的可信度？这涉及到假设检验的两类错误的理解，以及衍生出来的功效分析。

假设检验的两类错误

统计假设检验中，我们会先设定原假设（$H_0$)，并同时设立它的对面，称为备择假设（$H_1$)。那么我们根据检验来判断是否拒绝H0，与实际的H0真假，对应有4个组合，其中判断错误的两个组合则分别是第一类和第二类错误。具体如下表：

拒绝$H_0$ 不拒绝$H_0$
$H_0$为真 第一类错误($\alpha$) 正确 ($1-\alpha$)
$H_0$为假 正确($power=1-\beta$) 第二类错误($\beta$)
  • 第一类错误
    • 原假设是真的，但我们拒绝了它（误认为它是假的）
    • 对应假设检验的显著性水平($\alpha$)。
    • 这也是常被人称道的P值的对比标准，例如P值小于0.05则认为通过假设检验，拒绝XX相等的原假设，结论是XX有显著差异
  • 第二类错误
    • 原假设是假的，但我们没有拒绝它（误认为它是真的）
    • 当原假设为假，我们正确拒绝原假设的概率就是 1-第二类错误概率，对应假设检验的功效($power=1-\beta$)。
    • power一般设置0.8以上，才认为拒绝$H_0$的决策，具有足够的功效（这个往往被人遗忘)

alpha和power的详解

举个实例来阐述alpha和power：一家公司更新了销售策略，希望知道单价是否有显著提升，原来的客单价30元/人，公司认为提升到32元/人的课单价才认可新策略。现在收集到了新策略下的n个样本，需要针对这批样本做假设检验，那么要检验的假设如下：

  • 原假设 $H_{0}:\mu=30$
  • 备择假设 $H_{1}: \mu=32$

根据原假设和备择假设，可以分别画出分布图如下：

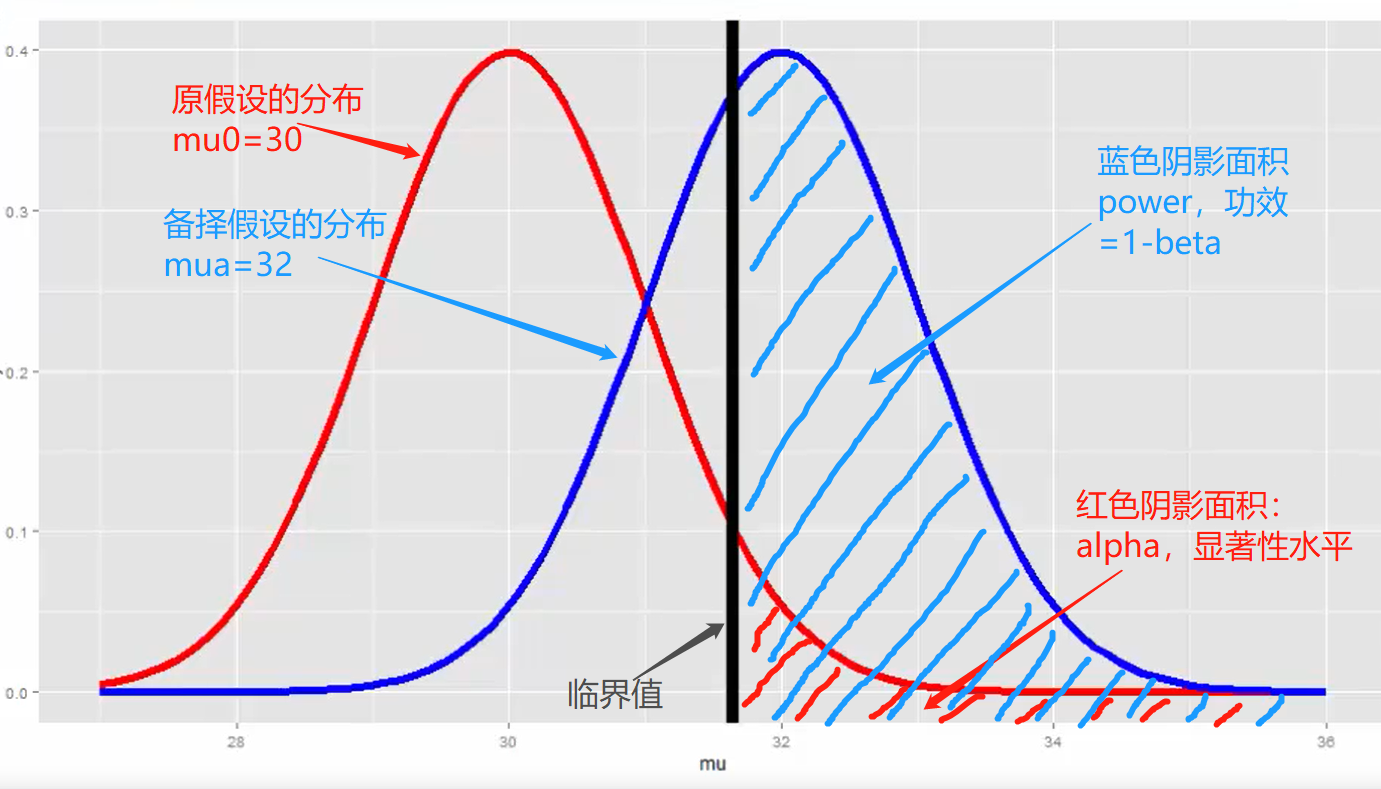
显然，这个示例需要使用均值T检验，给定显著性水平后，就能根据分布推出临界值，即如果n个样本计算出的T统计量落在图中黑线右侧，则拒绝原假设,犯第一类错误的概率为红色阴影面积(alpha)，而接受备择假设的正确率则为蓝色阴影面积（power）。

上述T检验对应alpha和power具体的计算公式如下（即只有分布均值$\mu$的差异，注意求$\beta$的是非中心化的t分布）：

  • $ \alpha=P\left(\frac{\bar{X}-30}{s / \sqrt{n}}>t_{1-\alpha, n-1} ; \mu=30\right) $
  • $ 1-\beta=P\left(\frac{\bar{X}-30}{s / \sqrt{n}}>t_{1-\alpha, n-1} ; \mu=32\right) $

样本量的计算

铺垫这么多，终于能讲样本量的计算了。上一部分T检验的功效公式，可以看到，功效除了和样本分布、显著性水平有关，还和样本量$n$有关。因此实际假设检验中有4项相互依赖的指标：

  • 显著性水平,P(第一类错误)
  • 功效，1-P(第二类错误)
  • 样本大小，n
  • 效应值（例如上面效应值定义为$(32-30)/\sigma$)

以上4个指标确定其中三个即可计算出第四个。于是我们要预估假设检验所需的样本量，则需要先给定另外三项的取值，再代入公式计算即可。不同类型的假设检验都有不同的公式，此处不再赘述。

代码示例

R语言中，直接使用library(pwr)包即可实现各类检验的功效分析。以工作中最常见的两个检验（均值T检验和比例检验）为例，代码如下：

示例-均值T检验

以上面的为例，假设根据过去经验知道客单价的标注差为4，想要验证客单价从30提升到了32，在显著性水平为0.05，功效为0.9的标准下，对应需要样本量n：

1
2
library(pwr)
pwr.t.test(d=(32-30)/4,sig.level = 0.05,power = 0.9,type = 'one.sample',alternative = 'greater')

结果显示，要达到以上标准，至少需要36个样本（注意，效应值为d=(32-30)/4，由于只有一组数据，所以是单样本检验’one.sample’，由于只对客单价提高感兴趣，因此只需单边检验 alternative = greater）

1
2
3
4
5
6
7
# One-sample t test power calculation 
# 
# n = 35.65269
# d = 0.5
# sig.level = 0.05
# power = 0.9
# alternative = greater

示例-比例检验

某公司想对比两个策略下（一个是对照组，一个是测试组）的转化率是否有显著差异，按照历史经验知道对照组的转化率是0.2，而测试组的目标转化率是提升到0.25），在显著性水平为0.05，功效为0.9的标准下，对应每个组需要样本量n：

1
pwr.2p.test(h=ES.h(0.25,0.2),sig.level = 0.05,power = 0.9,alternative = 'greater')

结果显示，要达到以上标准，至少需要1191个样本。（注意，效应值为ES.h(0.25,0.2)）

1
2
3
4
5
6
7
8
9
# Difference of proportion power calculation for binomial distribution (arcsine transformation) 
# 
# h = 0.1199023
# n = 1191.362
# sig.level = 0.05
# power = 0.9
# alternative = greater
# 
# NOTE: same sample sizes

以上即为确定目标和检验标准之后需要的样本量预估。特别提醒，对效应值的预估是最重要的，alpha和power一般都设置0.05~0.1,0.8~0.9即可，而效应值代表了对该实验目标的界定，如果设定的目标虚高，例如上面的测试组转化率要达到0.5，那么对应每组样本量只需要41个，而实际上测试组样本显示只有0.3的转化率，那么在给定这些的情况下算出来power必然小于设定值：

1
2
# 样本显示两个组转率是0.3和0.2，因此效应值为h=ES.h(0.3,0.2)
pwr.2p.test(h=ES.h(0.3,0.2),sig.level = 0.05,n=41,alternative = 'greater')

结果显示，0.3和0.2比例下的power只有0.28，因此必须继续放量试验，扩大样本量从而提高power。

1
2
3
4
5
6
7
8
9
# Difference of proportion power calculation for binomial distribution (arcsine transformation) 
# 
# h = 0.2319843
# n = 41
# sig.level = 0.05
# power = 0.2760888
# alternative = greater
# 
# NOTE: same sample sizes

References