简介
模型评估通常作为建模的最后一步,用于评估模型效果,判别该模型是否达到预期。但实际模型评估指标需要在建模的第一步确定,即确定目标函数。凡事都得有个目标,才知道努力的(拟合)方向,否则枉然。
连续值或者分类型的预测最常用的说法就是模型精度,但实际精度一词有多重含义,例如连续性预测模型常用的是MAPE/RMSE,而分类常用AUC/accuracy/recall/specify等等。本文将介绍常用的评估指标,并对应下各指标的不同称呼。
0-1分类预测的评估
一般的分类都是二元分类,而最常用的则是ROC曲线下方的面积AUC值了。首先需要知道混淆矩阵的构成,以及其衍生的一系列评估指标,取其不同阈值下的两个评估指标,即可构成ROC曲线,而曲线下方的面积,即为AUC值。
混淆矩阵
对于而分类问题,记1为正例,0为负例,预测和实际的值则会出现4中组合,例如,对某一样本,预测值为1(Positive),而实际值也为1,说明预测正确,即为 True Positive(真正例),反之如果实际值为0,则预测错误,即为 False Positive(假正例)。根据4中组合,得到混淆矩阵如下:
| 预测-1 | 预测-0 | ||
|---|---|---|---|
| 实际-1 | True Positive(TP) | False Negative(FN) | Actual Positive (P=TP+FN) |
| 实际-0 | False Positive(FP) | True Negative(TN) | Actual Negative (N=FP+TN) |
| Predicted Positive (P’=TP+FP) | Predicted Negative (N’=FN+TN) | TP+FP+FN+TN |
衍生的各种评估指标如下:
- 准确率(
accuracy)- $\frac{T P+T N}{TP+FP+FN+TN}$
- 错误率
- $\frac{FP+FN}{TP+FP+FN+TN}$
- 敏感度(
sensitivity)、真正例率、召回率(recall)- $\frac{TP}{TP+FN}$
- 特效性(
specificity)、真负例率- $\frac{TN}{FP+TN}$
- 精度(
precision)- $\frac{TP}{TP+FP}$
- $F_1$、F分数(精度和召回率的调和均值)
- $\frac{2 \times \text {precision} \times \text {recall}}{\text {precision}+r e c a l l} = \mathrm{F} 1=\frac{2 \mathrm{TP}}{2 \mathrm{TP}+\mathrm{FP}+\mathrm{FN}}$
- 实际来自于: $\frac{2}{\mathrm{F} 1}=\frac{1}{\mathrm{P}}+\frac{1}{\mathrm{R}}$
ROC曲线
分类模型的原始预测值是0~1之间的连续型数值,可理解为因变量取1的概率,一般取0.5作为阈值,即小于0.5记为预测的0,大于等于0.5记为预测的1;而实际上根据不同情况可以取不同的阈值。
例如,银行预测可能发生贷款逾期的账目,由于整体逾期率非常低,例如样本中100个只有1个逾期,如果只看准确率,那么全预测0(即,不逾期)则可达到99%的准确率,显然不妥,因此此时会秉着宁可错杀一千不可放过一个的原则,会将阈值适当降低,例如降到0.1,若大于0.1则预测为1。(实际上此时主要的评估指标会选择recall)。
用不同的阀值,统计出每组不同阀值下的精确率和召回率,
- 横坐标:假正率(
FPR,即1-specificity,1-真负例率)- FPR = FP /(FP + TN)
- 纵坐标:真正例率(
TPR, 即recall)- TPR = TP /(TP + FN)
即可画出ROC曲线(受试者工作特征曲线,receiver operating characteristic curve),示例(图片来源于他处)如下
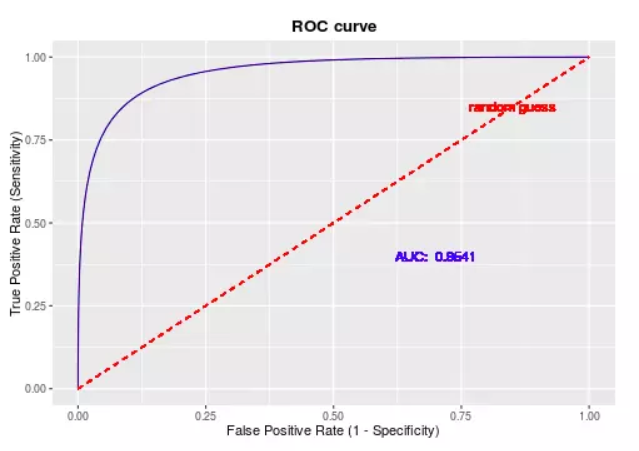
ROC曲线优势就是,当正负样本的分布发生变化时,其形状能够基本保持不变,因此其面积AUC值,可以说是极度适用于不平衡样本(例如以上的银行逾期数据,正负比极度不均衡)的建模评估了。AUC越大,模型分类效果越好,一般来说,AUC低于0.7的模型基本上是个废柴了。(若在正负样本比1:1情况下全预测为0或者1,AUC即为0.5)
R语言实现
可使用ROCR包计算AUC值,混淆矩阵自己写即可,代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31library(ROCR)
get_confusion_stat <- function(pred,y_real,threshold=0.5){
# auc
tmp <- prediction(as.vector(pred),y_real)
auc <- unlist(slot(performance(tmp,'auc'),'y.values'))
# statistic
pred_new <- as.integer(pred>threshold)
tab <- table(pred_new,y_real)
if(nrow(tab)==1){
print('preds all zero !')
return(0)
}
TP <- tab[2,2]
TN <- tab[1,1]
FP <- tab[2,1]
FN <- tab[1,2]
accuracy <- round((TP+TN)/(TP+FN+FP+TN),4)
recall_sensitivity <- round(TP/(TP+FN),4)
precision <- round(TP/(TP+FP),4)
specificity <- round(TN/(TN+FP),4)
# 添加,预测的负例占比(业务解释:去除多少的样本,达到多少的recall)
neg_rate <- round((TN+FN)/(TP+TN+FP+FN),4)
re <- list('AUC' = auc,
'Confusion_Matrix'=tab,
'Statistics'=data.frame(value=c('accuracy'=accuracy,
'recall_sensitivity'=recall_sensitivity,
'precision'=precision,
'specificity'=specificity,
'neg_rate'=neg_rate)))
return(re)
}
引用上篇lasso-R示例博文的评估结果示例如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16# $AUC
# [1] 0.8406198
# $Confusion_Matrix
# y_real
# pred_new 0 1
# 0 20 8
# 1 32 131
# $Statistics
# value
# accuracy 0.7906
# recall_sensitivity 0.9424
# precision 0.8037
# specificity 0.3846
# neg_rate 0.1466
连续值预测的评估
连续型变量的预测,通常使用MAPE和RMSE。对于回归问题的模型还经常使用拟合优度 $R^2$ 作为评估指标。
MAPE
MAPE(mean absolute percentage error)为平均百分比误差,预测连续型数据的准确率一般指1-MAPE,例如预测未来10个月的GDP数据,准确率达到98%,即代表该模型的预测 MAPE 为2%。
$$MAPE=\sum_{t=1}^{n}\left|\frac{\text {observed}_{t}-\text {predicted}_t}{\text {observed}_t}\right| \times \frac{100}{n}$$
MSE/RMSE
RMSE(root mean square error)为均方根误差,相应的MSE(mean square error)即为误差的平方和,两者含义一致,指标越小则模型效果越好。
$$RMSE=\sqrt{\frac{1}{N} \sum_{t=1}^{N}\left(\text {observed}_t-\text {predicted}_t\right)^{2}}$$
拟合优度
拟合优度(Goodness of Fit)是指回归直线对观测值的拟合程度。
R²/可决系数
度量拟合优度的统计量是可决系数(亦称确定系数)R²。R²的值越接近1,说明回归直线对观测值的拟合程度越好;反之,R²的值越小,说明回归直线对观测值的拟合程度越差。R²等于回归平方和( explained sum of squares)在总平方和( total sum of squares)中所占的比率,即回归方程所能解释的因变量变异性的百分比。
注意,回归问题才能用R²衡量
$$ R^{2} = \frac{S S_{\mathrm{reg}}}{S S_{\mathrm{tss}}}=1-\frac{S S_{\mathrm{rss}}}{S S_{\mathrm{tss}}} = 1- \frac{\sum_{i}\left(y_{i}-f_{i}\right)^{2}}{\sum_{i}\left(y_{i}-\bar{y}\right)^{2}} $$
由以上公式实际上可知,在带有截距项的线性最小二乘多元回归中(注意这个前提条件),$R^2$就是预测值和实际值相关系数的平方,即(注意,一定是线性回归模型才行):
$$ R^{2}=cor(y_{real},y_{fit})^{2} $$
调整的R²
在模型中增加多个变量(即使是无实际意义的变量)也能小幅度提高R平方的值,因此需要考虑模型的变量数作为相应惩罚,于是得到调整的R²如下:
$$ R_{adjusted}^{2} =1-\frac{S S_{\mathrm{rss}}/(n-p-1))}{S S_{\mathrm{tss}}/(n-1)}$$
R语言实现
1 | # MAPE |